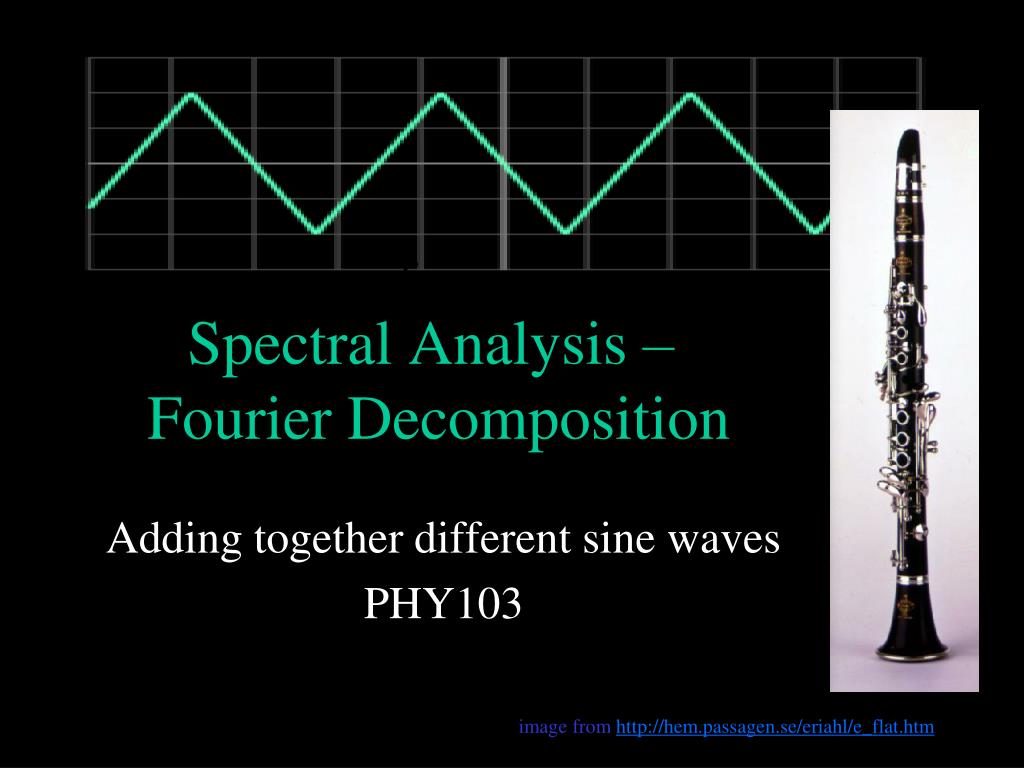
Spectral Analysis – Fourier Decomposition
Adding together different sine waves PHY103
f
image from http://hem.passagen.se/eriahl/e_flat.htm
Spectral decomposition Fourier decomposition
- Previous lectures we focused on a single sine wave.
- With an amplitude and a frequency
- Basic spectral unit —- How do we take a complex signal and describe its
frequency mix? We can take any function of time and describe it as a
sum of sine waves each with different amplitudes and frequencies
Sine waves – one amplitude/ one frequency
Sounds as a series of pressure or motion
variations in air. Sounds as a sum of different amplitude
signals each with a different frequency. Waveform vs Spectral view in Audition
Spectral Clarinet spectrum view
Clarinet spectrum with only the lowest harmonic remaining
Time →
Frequency
Waveform view
Full sound Only lowest harmonic
Four complex tones in which all partials have been removed by filtering (Butler Example 2.5)
One is a French horn, one is a violin, one is a pure
sine, one is a piano (but out of order)
It’s hard to identify the instruments. However clues
remain (attack, vibrato, decay)
Making a triangle wave with a sum of harmonics.
Adding in higher frequencies makes the triangle tips sharper and sharper.
From Berg and Stork
Sum of waves
- Complex wave forms can be reproduced with a sum of different amplitude sine waves
- Any waveform can be turned into a sum of different amplitude sine waves “Fourier decomposition – Fourier series”
What does a triangle wave sound like compared to the square wave and pure sine wave?
- (Done in lab and previously in class)
- Function generators often carry sine, triangle and square waves (and often sawtooths too) If we keep the frequency the same the pitch of these three sounds is the same. However they sound different. Timbre — that character of the note that enables us to identify different instruments from their sound. Timbre is related to the frequency spectrum.
Same harmonics however the higher order harmonics are stronger.
Square wave sounds shriller than the triangle which sounds shriller than the sine wave From Berg and Stork
Square wave
Which frequencies are added together?
f frequency
5f 3f
To get a triangle or square wave we only add sine waves that fit exactly in one period. They cross zero at the beginning and end of the interval.
These are harmonics.
Periodic Waves
- Both the triangle and square wave cross zero at the beginning and end of the interval.
- We can repeat the signal Is “Periodic”
- Periodic waves can be decomposed into a sum of harmonics or sine waves with frequencies that are multiples of the biggest one that fits in the interval.
Sum of harmonics
- Also known as the Fourier series
- Is a sum of sine and cosine waves which have frequencies f, 2f, 3f, 4f, 5f, ….
- Any periodic wave can be decomposed in a Fourier series
Building a sawtooth by waves
- Cookdemo7 a. top down b. bottom up
Light spectrum
Image from http://scv.bu.edu/~aarondf/avgal.html
Time
Sound spectrum e
dutilpmaf 3f 5f 7f frequency
Sharp bends imply high frequencies
Leaving out the high frequency components smoothes the curves Low pass filter removes high frequencies – Makes the sound less shrill or bright
Sampling
If sampled every period then the entire wave is lost
The shorter the sampling spacing, the better the wave is measured — more high frequency information
More on sampling
Two sample rates A. Low sample rate that distorts the original sound wave. B. High sample rate that perfectly reproduces the original sound wave. Image from Adobe Audition Help.
Guideline for sampling rate
- Turning a sound wave into digital data: you must measure the voltage (pressure) as a function of time. But at what times?
- Sampling rate (in seconds) should be a few times faster than the period (in seconds) of the fastest frequency you would like to be able to measure
- To capture the sharp bends in the signal you need short sampling spacing
- What is the relation between frequency and period?
Guideline for choosing a digital sampling rate
Period is 1/frequency
Sampling rate should be a few times shorter than 1/(maximum frequency) you would like to measure For example. If you want to measure up to 10k Hz. The period of this is 1/104 seconds or 0.1ms. You would want to sample at a rate a few times less than this or at ~0.02ms.
Recording in Audition
The most common sample rates for digital audio editing are as follows:
- 11,025 Hz Poor AM Radio Quality/Speech (low-end multimedia)
- 22,050 Hz Near FM Radio Quality (high-end multimedia)
- 32,000 Hz Better than FM Radio Quality (standard broadcast rate)
- 44,100 Hz CD Quality
- 48,000 Hz DAT Quality
- 96,000 Hz DVD Quality
Demo –degrading sampling and resolution
- Clip of song by Lynda Williams sampling is 48kHz resolution 16 bit
- 48kHz sampling , 8 bit
- 11kHz sampling, 16bit
Bits of measurement
8 bit binary number 00000000b = 0d 00000001b = 1d 00000010b = 2d 00000011b = 3d 00000100b = 4d … 11111111b = 511d
can describe 2^8 = 512 different levels
sampling
Error in amplitude of signal loudness error error in recording the strength of signal
Bit of precision
Bits of measurement
A signal that goes between 0Volt and 1Volt
- 8 bits of information
- You can measure 1V/512 = 0.002V = 2mV accuracy
- 16bits of information 2^16 = 65536
- 1V/65536= 0.000015V = 0.015mV = 15micro Volt accuracy
Creating a triangle wave with Matlab using a Fourier series dt = 0.0001; % sampling time = 0:dt:0.01; % from 0 to 0.01 seconds total with sampling interval dt % Here my sample interval is 0.0001sec or a frequency of 10^4Hz frequency1 = 440.0; % This should be the note A % harmonics of this odd ones only frequency2 = frequency1*3.0; frequency3 = frequency1*5.0; frequency4 = frequency1*7.0; % here are some amplitudes a1 = 1.0; a2 = 1.0/9.0; a3 = 1.0/25.0; a4 = 1.0/49.0; % here are some sine waves y1 = sin(2.0*pi*frequency1*time); y2 = sin(2.0*pi*frequency2*time); y3 = sin(2.0*pi*frequency3*time); y4 = sin(2.0*pi*frequency4*time); % now let’s add some together y = a1*y1 – a2*y2 + a3*y3 – a4*y4; plot(time, y); % plot it out
Playing the sound
%Modify the file so the second line has time = 0:dt:2; %(2 seconds) %Last line: play it: sound(y, 1/dt) Save it as a .wav file for later wavwrite(0.8*y,1/dt,’triangle.wav’)
Phase
Up to this point we have only discussed amplitude and frequency
x = 0:pi/100:2*pi; y = sin(x); y2 = sin(x-.25); y3 = sin(x-.5); plot(x,y,x,y2,x,y3)
period
amplitude
phase
Sine wave
What happens if we vary the phase of the components we used to make the triangle wave?
y1 = sin(2.0*pi*frequency1*time); y2 = sin(2.0*pi*frequency2*time – 1.6); y3 = sin(2.0*pi*frequency3*time – 0.1); y4 = sin(2.0*pi*frequency4*time +1.3); y = a1*y1 + a2*y2 + a3*y3 + a4*y4;
Shape of wave is changed even though frequency spectrum is the same
Is there a difference in the sound?
These two are sums with the same amplitude sine waves components, however the phases of the sine waves differ.
Another example
This sound file has varying phases of its frequencies. Do we hear any difference in time?
Sound file from http://webphysics.davidson.edu/faculty/dmb/py115/MusTechS05.htm
Spectrum of this sound
Waveform views at different times
Do we hear phase?
Helmholtz and Ohm argued that our ear and brain are only sensitive to the frequencies of sounds. Timbre is a result of frequency mix. There are exceptions to this (e.g., low frequencies) Two major psycho-acoustic models 1) Place theory – each spot in basal membrane is sensitive to a different frequency 2) Timing – rate of firing of neurons is important and gives us phase information What is the role of each in how our ear and brains process information? Open questions remain on this.
Cutting and pasting audio
High frequencies introduced
Phase shift
Sharp changes in wave form
Demo with a cut and paste in Audition/Audacity of a generated sine. Note: the effect in spectral view depends on the length of the FFT used, also you need to be fairly zoomed out horizontal to see the noise.
Transform and inverse transform
f 3f 5f 7f frequency e dutilpmaTime
I have shown how to go this way
How we will talk about how to take a signal and estimate the strength of its frequency components
Multiplying two cosines with different frequencies
Multiplying two cosines with the same frequency
The average is not zero.
The average is 1/2
Multiplying two cosines with different frequencies
What if your window fits here?
Windowing and errors
Calculating the amplitude of each Fourier component
What is the average of
Over a long interval this averages to zero unless f=g Sine/Cosine functions are “orthogonal”
Calculating the amplitude of each Fourier component
- Procedure: multiply the waveform f(t) by a cosine or sine and take the average.
- Multiply by 2. This gives you the coefficient Am or Bm.
Predicting the spectrum of a plucked string
- Can one predict the amplitude of each mode (overtone/harmonic?) following plucking?
- Which pluck will contain only odd harmonics?
- Which pluck has stronger higher harmonics?
Odd vs Even Harmonics and Symmetry
- Sines are Anti- symmetric about mid-point
- If you mirror around the middle you get the same shape but upside down
More on Symmetry
- Sines are anti- symmetric
- Cosines are symmetric
n=1 odd
n=3 odd
n=2 even
Symmetry
- Additional symmetry of odd sines if you consider reflection at the black line.
- About this line, Odd harmonics are symmetric but even ones are anti- symmetric
Symmetry of the triangle wave
Obeys same symmetry as the odd harmonics so cannot contain even harmonic components
Odd Fourier components
Both triangle waves and square waves contain odd Fourier components.
e dutilpmaf 3f 5f 7f frequency
Sawtooth
- What overtones are present in this wave? Use its symmetry to guess the answer.
Spectrum of sawtooth
All integer harmonics are present. The additional symmetry about the 1⁄4 wave that both triangle and square wave have is not present in the sawtooth.
Generated tones
Order of 440Hz tones:
Sine, Triangle, Sawtooth, Square, Rectangular with 10%/90%
Sawtooth
Triangle
Symmetry as a compositional element
- From Larry Solomon’s “Symmetry as a compositional element” — last phrase of Bartok’s Music for Strings, Percussion and Celesta, movement I
- Reflection symmetry in tones — axis of symmetry is an A
- microcosmos vol 6 141 Free variations
Reflection in time
Axis of symmetry is a time
(Example from Larry Solomon) Anton Webern, Opus 27
Predicting the spectrum of a plucked string
- Can one predict the amplitude of each mode (overtone/harmonic?) following plucking?
- Using the procedure to measure the Fourier coefficients it is possible to predict the amplitude of each harmonic tone.
Predicting the spectrum of a plucked string
- You know the shape just before it is plucked.
- You know that each mode moves at its own frequency
- The shape when released
- We rewrite this as
Predicting the motion of a plucked string (continued)
Each harmonic has its own frequency of oscillation, the m-th harmonic moves at a frequency or m times that of the fundamental mode.
Moving string in general
Does this make sense? Some checks:
Are left and right boundaries fixed?
Is the string not moving at t=0?
Sum of forward + backwards travelling waves
Initial condition given above, and the velocity every where is zero. This is equal to the sum of two traveling waves
Shape of wave form can be predicted at future times by considering each traveling wave and how it reflects off of the boundaries
Violin and stick slip motion
Figure and animation from http:// www.phys.unsw.edu.au/jw/Bows.html
Each line scanned at a different time.
The “rolling shutter” Between 24 and 30fps. 1280 x 720 pixels At fastest 0.033s per frame If I divide by 1/1000 then ~ 30 microseconds delay between lines
Iphone films
- http://www.wired.com/gadgetlab/2011/07/ iphones-rolling-shutter-captures-amazing- slo-mo-guitar-string-vibrations/
Guitar string
- Length of string, L, is about a meter, frequency of lowest string is 82Hz, P=0.012s
- Speed on the string v/(2L) = f → v = 2Lf ~160 m/s
- The delay between lines is 30 microseconds corresponding to a distance of 160m/s x 30 microseconds = 5e-3m = 0.5cm
- Number of lines to get there and back travel times 0.012/33e-6=400 (half the picture) as expected
- Maybe could do this calculation more efficiently by considering what fraction of wavelength fits in view of camera, giving phase information
Clarinet spectrum
172 Hz
506 Hz 333 Hz
172*2=344
172*3=516
Why is the third harmonic stronger than the second?
1094Hz 347Hz 697Hz
1396Hz
Even harmonics are the same size
Piano spectrum
347*2=694 347*3=1041 347*4=1399
Piano spectrum
- C4 piano on left, sawtooth at same frequency on right.
- High overtones are higher in piano.
- Why?
Are these frequency shifts important?
Butler (example 2.4). a) Piano playing C4 b) Piano playing C4 but the partials have been lowered by digital processing so that their frequencies are exact integer multiples of the fundamental. Pair of tones repeated 3 times.
Synthesized voicing
- Voice and many instruments make a nearly periodic signal
- Overtones are all integer multiples of each other
- Frequencies are fixed
- However if a tone is synthesized to have exact integer overtones and fixed frequencies it sounds electronic
- How do you synthesize more realistic tones?
Irregularities are important
- Slight frequency shifts
- Slight timing differences in the periodic waveform
Timing differences from turbulence in throat and other sources. If there is no irregularity then the tones are unnatural and dull.
Synthesized singer
Cookdemo70
- No vibrato b. Random and periodic vibrato and singer
scooping slightly upward at beginning of each note
Nearly Periodic Waveforms
- Voice, guitar, flute, horn, didgeridu, piano: all have ladder spectrum Why nearly periodic signals?
- Stringed instruments. Modes of vibration have frequencies that are integer multiples of a fundamental tone. All modes are excited by plucking. Harmonics are modes.
- Wind instruments. Mode frequencies are close to integer multiples of a fundamental. Excitation builds on one mode. Excitation (mouth) is nearly periodic. Resulting sound contains harmonics. The harmonics may not be modes. Sometimes other modes can be seen in the sound spectrum that are not harmonics.
- Voice. Excitation is nearly periodic. Tract resonances give formants, but not key toward driving sound. Emerging sound since nearly periodic contains harmonics. Not all musical sounds are nearly periodic in nature
Some history
Images and information from http://physics.kenyon.edu/ EarlyApparatus/Rudolf_Koenig_Apparatus/ Helmholtz_Resonator/Helmholtz_Resonator.html
Earliest sound spectra taken by Helmholtz ~1860 who used glass spheres or cylinders, each with a difference size and hole diameter setting its resonant frequency. The opposite side would have a slender opening that could be held in the ear. The enclosed volume of air acts as a spring connected to the mass of the slug of air, and vibrates in an adiabatic fashion at a frequency dependent on the density and volume of the air, its molecular composition, and the mass of the slug of air in the neck.
- Sets of these were built and ordered by universities to allow spectra of sounds to be measured in the lab
- This very large set of twenty two Helmholtz resonators is in the Garland Collection of Classic Physics Apparatus at Vanderbilt University. These were bought by Chancellor Garland to outfit the Vanderbilt physics department for the opening of the university in 1875. Garland had previously gone to visit Koenig in Paris to discuss his order. in 1889 a set of nineteen resonators cost 170 francs.
Tunable resonators
- a cylindrical resonator permits the volume of the resonator to be changed by sliding the tubes in and out. The notes (and hence the resonant frequencies) are engraved on the side of the apparatus. This is one of a number of tunable Helmholtz resonators at the University of Vermont.
Tunable resonators
Ocarinas and whistling
Unlike with flutes the pitch is not set by the effective length of the instrument
Whistle
- To do : film a whistle of across an octave
Fourier analysis in 1890
- « Manometric Flame Analyser for the timbre of sounds, with 14 universal resonators — originally 650 francs » ($130). The adjustable Helmholtz resonators are tuned to the fundamental frequency of the sound to be analyzed, plus its harmonics. The holes on the other side of the resonators are connected by the rubber tubes to manometric flame capsules, and the variation in the height of the flames observed in the rotating mirror. The variation is proportional to the strength of the Fourier component of the sound.
- The picture at the left, below, shows the manometric capsules and the jets where the flames are produced. Note the black background to made the flames more visible.
- BTW nice display at U Toronto!
Now how is the frequency analysis computed?
- The fast Fourier transform (FFT) is a discrete Fourier transform algorithm which reduces the number of computations needed for N points from 2N2 to 2Nlog2N computations
- Discrete: works on data points rather than a function.
- A nice, space efficient algorithm exists for the number of points N equal to a power of 2.
- When you do a frequency analysis in Adobe Audition one of the parameters you can choose is N (and you will notice that the menu only allows powers of 2).
The FFT algorithm
- A nice, memory efficient algorithm exists if the number of points is a power of 2
- Each component can be written as a sum of components from a transform of the interval divided in half.
- It maybe makes sense that the number of steps depends on log N
Taking an FFT
- Total interval P
- Number of points N
- Sampling dt
- P=N*dt
- Windowing function – entire interval is multiplied by a function
dT
P
télécharger gratuitement cours de Spectral Analysis –Fourier Decomposition